OpenFOAMユーザーズグループで投稿のあった、回転円筒容器内の水面挙動に関し、MRFInterFOAMを使って計算する方法について調べてみた。⇒確かに、なかなか一筋縄で計算できるものでなかったようで、本稿(その1)では、まずは計算してみた篇です。
普通に予想される結果(放物面状の液面)とは異なっていますが、一概にまるでおかしい・・・とも言い切れない面があると思います。どうでしょう?少し偏心して回転すると、これに似た挙動をしてくれそうな気もします(実は、ビール造りで、大きなバケツ状タンクに投入した酵母イーストを攪拌する際によく経験しています)。
最後のほうで、何故こうなったのか、どうすれば予想結果が得られそうかの考察をしていますが、まずはここまで、普通にやればこうなったというところを、以下具体的にどうやって計算したかの解説です。
なお、あちらではsnappyHexMeshでメッシュ作成していましたが、こちらではblockMeshのみでやりました。(当初、提示されていたモデルではメッシュが辛そうだったので)
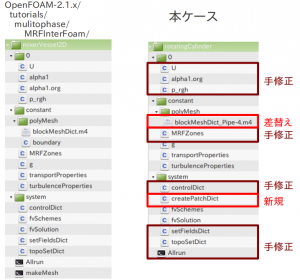
チュートリアルケースの変更概要
基本的なやり方は、チュートリアルケース(tutorials/multiphase/MRFInterFoam/mixerVessel2D)をそのままコピーしてケース名を変更、一部のファイルを変更するという作業です。ファイル別に、実施した修正作業の全体概要を以下に示しておきます。
以下、修正内容の要点を記しておきます。
メッシュ作成
メッシュ作成には、拙作のブロックメッシュ作成マクロを使いました。
マクロファイル(*.m4)をblockMeshDictのあるpolyMeshフォルダと同じ場所に置いておけば、ケースのルートフォルダにて、以下のコマンドを実行すれば、メッシュの出来上がりです。
$ m4 < constant/polyMesh/blockMeshDict_Pipe-4.m4 > constant/polyMesh/blockMeshDict
$ blockMesh
マクロのパラメタ設定部分
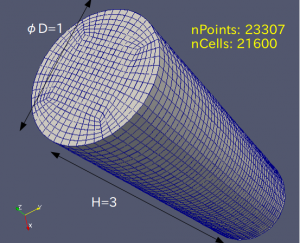
メッシュの出来上がりイメージ
境界定義
あちらでは、上面を開口にしていましたが、ここでは(面倒なので)全周壁面としての計算にした。多分、あんまり結果は変わらないんではないかと・・・
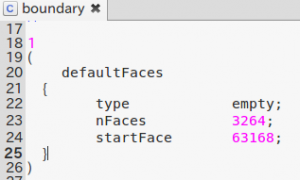
上の方法で作成したメッシュの境界(constant/polyMesh/boundary)は、全面がdefaultFaces(type empty)となっているので、
これを、walls (type wall) に変更する。手修正も簡単だが、メッシュを変更の都度やり直すのは面倒だし、自動化もやりたい。ここはcreatePatchコマンドでやることにした。
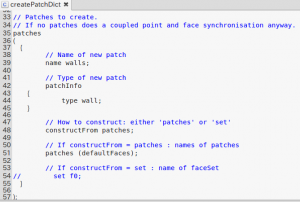
systemフォルダの下に、以下の内容のcreatePatchDictを仕込んでおけば、
以下のコマンド実行で、一発変換してくれます。
$ createPatch
境界条件
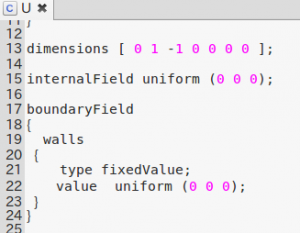
流速
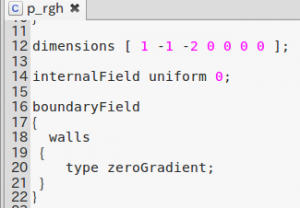
圧力
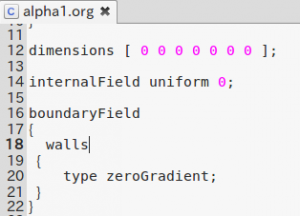
液体比率
回転領域の設定
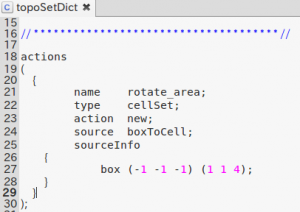
MRF(Multi Reference Frame)系のソルバーを使うには、回転領域に相当する部分のセルにVolume名をつけておく必要がある。色々なやり方があるが、ここではtopoSetコマンドを用いる。
systemフォルダの下に、以下の内容のtopoSetDictを仕込んでおけば、
$ topoSet
$ setsToZone -noFlipMap
というコマンドにて、全領域に、rotate_area というVolume名が付けられることになります。
初期水面高さの設定
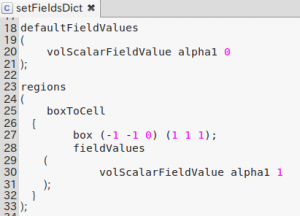
水面の初期状態はsetFieldコマンドにて設定します。systemフォルダの下に、以下のsetFieldDict を仕込んでおけば、
$ cp 0/alpha1.org 0/alpha1
$ setField
にて、z方向高さ1メートルの部分までが、水(alpha1=1)で満たされたことになる。
回転条件の設定
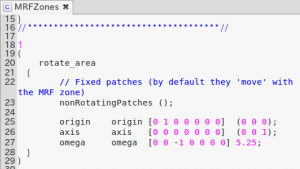
回転条件は、constantフォルダの下の、MRFZonesファイルで記述しておく
原点(0 0 0)を通る、z軸(0 0 1)回りに、5.25 rad/s ということです。
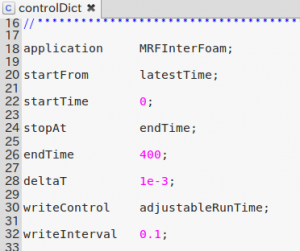
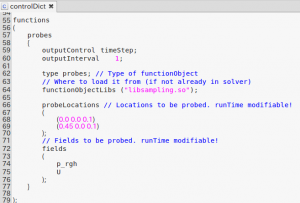
計算制御(controlDict)
endTimeが400と非常に大きい値にしてあります。チュートリアルケースでは4でした。なので、途中でリスタート計算できるよう、
sttartFrom latestTime;
と変更しました。
writeIntervalは、0.1くらいにしておかないと、アニメーション表示に耐えられません(0.1secで30degほどの回転角になってしまうので)。400secの計算ともなると、4000コマの出力になってしまいます。ここはご自分の環境にあわせて書き換えて下さい。
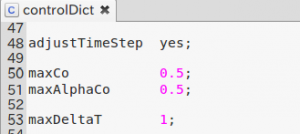
deltaTは1e-3となっていますが、あくまで初期値です。以下、
にて、自動時間刻みで計算は進行します。この部分の値は、チュートリアルケースの値を変更していません。
最後に、function probe を追加しています。
底面の上方0.1メートルの中心部(0.0 0.0 0.1)と外周部(0.45 0.0 0.1)における流速(U)と圧力(p_rgh)を全計算ステップにてモニター出力します。
これがないと、計算が準定常状態になったかどうかの判断が出来なかったからです。
計算実行
添付のAllrunを実行するだけです。
#!/bin/sh
m4 < constant/polyMesh/blockMeshDict_Pipe-4.m4 > constant/polyMesh/blockMeshDict
blockMesh
createPatch -overwrite
topoSet
setsToZones -noFlipMap
cp 0/alpha1.org 0/alpha1
setFields
MRFInterFoam | tee log.MRFInterFoam# —————————————————————– end-of-file
計算結果の概要
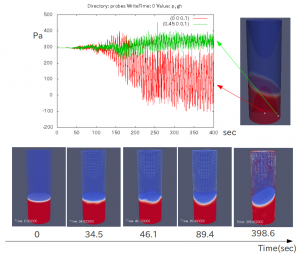
上段に前述のprobe点における圧力履歴をプロットし(緑色が外周、赤色が中央)、下段に任意の時刻における液面を表示しています。
このように、回転が始まってから30sec(約25回転)まで、ほとんど変化らしいものは見られず、35secくらいで、ようやくさざ波のようなものが現れて、それが次第に大きくなる。300secを過ぎたあたりでようやく準安定状態といってよさそうです。
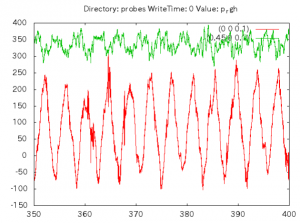
probe点圧力履歴を、350-400sec間だけプロットし直したのが下の図です。
この図から読み取って、最後の2周期分、約8sec間0.1sec毎のデータで作成したのが、冒頭に掲載したアニメーションです。
ちなみに計算時間は単体計算で約6時間
供試マシンは、ちょっと前の記事にて紹介したLinuxマシン
CPU:Core-i7 950
Memory:24GB
OS:Ubuntu-10.04
上に構築したMint12ベースの仮想マシン(ubuntu-11.10 相当)でやりました。
何はともあれ、お試しあれ
右(⇒)フレームのDownLoadカラムの rotatingCylinder です。
考察
当初、通常のファンなどで実施するMRF計算の経験から、数回転から10回転分の計算をすれば出来るだろう・・・と思って、endTimeをチュートリアルと同じ(4sec)か、数倍(20sec)まで見ておけばよかろうと始めたのですが、まるで液面が変化しませんでした。メッシュや計算パラメタに誤りがあるのではないかと、あれこれ変更確認し、随分回り道をしましたが、結局計算時間が足りなかったということでした。
通常やっている内部にファンを配したような計算では、内部物体表面の移動境界条件によって、流体の回転方向対流が生じることになりますが、本ケースの場合は、壁面の摩擦だけで流体を回転させることになるので、流体全体の回転運動が生じるようになるまでは相当の時間が必要になるということのようです。
ただ、ようやく計算できたとはいえ、冒頭に記したように予想した液面が放物面状にはなってくれませんでした。この結果が必ずしも不合理ではないかもしれないとしても、何故こういうことになったのかを考えると、本現象のレイノルズ数的なもの(慣性力/粘性力の比を代表する指標)を見ていく必要がありました。
たとえば、代表寸法を、円筒の直径(D=1)、代表速度を周速(U=RΩ,R=0.5,Ω=5.25)として考えると、
nu nu [ 0 2 -1 0 0 0 0 ] 1e-06;
なので、
Re=UD/nu
=2R^2Ω/nu
=0.5 x 10e6
と、非常に大きな慣性力支配の現象になっているということがわかります。なので粘性力による回転流れが出る前に慣性力による振動が出てしまう。そういう流れを層流計算している・・・という点にも無理があったということかもしれません。
したがって、予想した放物面の液面形状を得るには、以下2つのアプローチが考えられます。(他にもあるかもしれませんが・・・)
- 低レイノルズ数計算
- 乱流計算
以下、(その2)へ続く。(近日公開予定)